公式の覚え方
まずは公式の覚え方について解説します。初めに断っておきますが、これは全ての公式に当てはまる覚え方ではありません。
まず、色々な公式を眺めてみると、かなりの公式が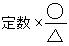
という形をしていることに気付きます。場合によっては定数や分母がないばあいもありますが、それも含めてこの形とみなす事が出来ます。
それで、これを利用した覚え方ですが、おいらは３段階方式で覚えました。どういうことかというと、まず公式に出てくる要素(文字)を考える、各要素が分母か分子かを判断する、公式全体の形を覚えるという３段構えです。
これについて、静電気力の式
を例にとって説明しましょう。まず、これが何に対する式かというと、二つの電荷の間に働く力の式です。だから、二つの電荷の間に働く力というものに関係しそうな要素を思い浮かべるわけです。そう考えると、二つの電荷の値そのもの、そして両者の間の距離が関係しそうだと言うことは納得できると思います。これが第一段階です。
そして、次に、これらの要素が分母か分子かを想像します。これを想像するには、分数の性質を知っている必要があります。分数は、分子が大きくなると大きくなり、分母が大きくなると小さくなります。そこで、それぞれの要素を大きくしたり小さくしたりと考えましょう。電荷の値が大きくなれば、おそらく力は大きくなるでしょう。よって電荷の値は分子にくると思われます。また、二つの間の距離が大きくなれば、力は小さくなることが想像できます。よってこの要素は分母にくるはずです。これが二段階目です。
最後に、各要素が二乗かどうか、定数は入るのか、係数は入るのか。これは覚えて貰うしかありません。
この三段階をよく読んでもらうと分かるのですが、覚えるという言葉は三段階目にしか出てきません。１、２段階目は記憶力はほとんど使わないで、想像力を使います。こうすることによって、単なる暗記ではなく、理解をしながら頭に入れるということが可能なのです。
公式の使い方
実際公式を覚えても、使い方が分からないとどうしようもありません。次に公式の使い方を解説します。といっても実は簡単で、公式は、一つ以外の文字の値が分かっている場合、その最後の文字を求めるのに使うのです。具体的に言うと、運動エネルギーの公式、E=m・ｖ２/２について、E=200J、ｖ＝10m/sと分かっているとき、この２つを式に代入すれば、２００=m・１０２となり、m＝４ｋｇと解けます。同様に、Eとmが分かっていればｖが、mとｖが分かっていればEが求まると言うわけです。
ということは、使える公式を探すときには、値のわからない物理量が一つあり、他の物理量が全て与えられたような公式を探せばよいわけです。但し、二つ以上値のわからない公式でも、ひとまず文字としておいて計算することが可能な場合がないわけではないです。