xがaからbまで
連続的に足す
F(x)について
F(x)+C
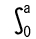 f(x)dx
f(x)dx奇関数なら0
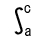 f(x)dx+
f(x)dx+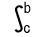 f(x)dx
f(x)dx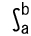 f(x)dx
f(x)dx=[f(x)g(x)]
-∫f(x)g'(x)dx
=∫f(g(t))g'(t)dt
積分区間も置換
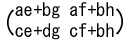
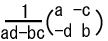
| F(b)-F(a) | f(x)dxを xがaからbまで 連続的に足す |
F'(x)=f(x)な F(x)について F(x)+C |
| 符号が反転 | 0 | (xn+1/n+1)+C |
| -(b-a)3/6 | 偶関数なら2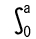 f(x)dx f(x)dx奇関数なら0 |
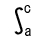 f(x)dx+ f(x)dx+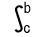 f(x)dx f(x)dx |
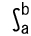 f(x)dx f(x)dx |
∫{f(x)-g(x)} | f(x) |
| sinx+C | -cosx+C | logx+C |
| (ax/loga)+C | ex | tanx+C |
| ∫π{f(x)}2dx | ∫f'(x)g(x)dx =[f(x)g(x)] -∫f(x)g'(x)dx |
∫f(x)dx =∫f(g(t))g'(t)dt 積分区間も置換 |
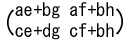 |
∫√1+{f'(x)}2dx | ∫√(df/dt)2+(dg/dt)2dt |
| AA-1=E | 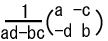 |
A2-(a+d)A+(ad-bc)E=O |