arn-1	(a+an)n/2 ＝{2a+(n-1)d}/2	a+(n-1)d
n(n+1)/2	n	a(rn-1)/(r-1)
a+bn	bn=an+1-an	n(n+1)(2n+1)/6
(x+y)n= nCrxn-rqr	n=1を証明 n=kを仮定し n=k+1を証明	an=Sn-Sn-1
△ABCで D,EがAB,ACの中点 ⇔DE//AC,2DE＝AC	三辺の比 二辺の比と夾角 二角相等	三辺 二辺夾角 一辺両端角相等
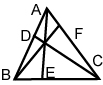(AD/DB)(BE/EC)(CF/FA)=1	△ABCで BM=MC→AB2+AC2 =2(AM2+BM2)	△ABCの ∠Aの二等分線と BCとの交点Dで AB:AC=BD:DC
対角の和が180°	中心角の半分 等しい弧に対する 円周角は等しい	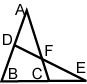(AD/DB) ×(BE/EC) ×(CF/FA)=1
内接円の中心 角の二等分線の交点	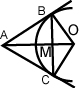AB=AC ∠BAM=∠CAM AO⊥BC BM=BC	接線と半径は垂直
外接円の中心 辺の垂直二等分線 の交点	辺の二等分線の交点 互いに他を2:1に内分	辺の垂線の交点
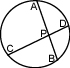	AP×PB =CP×PD	傍接円の中心 一つの内角と 二つの外角の 二等分線の交点