��P�@�ȉ��̕����萔�̎����������B
- �M�̃t���b�N�X
�@�@�t���b�N�X�Ƃ͒P�ʎ��ԓ�����A�P�ʖʐς�ʉ߂���ʂ������̂ŁA�M�̏ꍇ�́@�i��-2��-1
- �M�g�U�W��
�@�@�g�U�W���̓t���b�N�X�ƌ��z�����т���X���ł���A�����ړ��̏ꍇ�́A
�@�@�@�@�@�@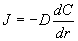
�@�@�Œ�`�����̂Ł@��2��-1
- ���S�x
���S�x�̕ʖ��͉^���ʊg�U�W���Ȃ̂ŁA�P�ʂ͊g�U�W���Ɠ����B ��2��-1
- �����ړ��W��
�t���b�N�X�́i�����ړ��W���j�~�i�Z�x���j�ŕ\����A�Z�x���̎����́mmol/��3�n�Ȃ̂ŁA ����-1
- ���C�W��
���C�W���͍R�͂ƕ��̂ɂ�����͂̔��W��\���W���ł���A�R�͂ƕ��̂ɂ�����͂̎����͓����Ȃ̂ŁA������
�@
��Q �ȉ��̗p��ɂ��āA�e�X�Q�`�R�s�Ő�������B
- ����
�ǂ�Ȃɗ��������������Ă������̕\�ʂ͎��̗͂��̗̂���ƈقȂ��đw���Ɏx�z����Ă��镔��������A��������E�w
�@�Ƃ����B���̋��E�w�̓����͑w���ɂ��g�U�Ŏx�z����Ă���A�����g�U�ɔ�ׂđ��x���x���̂ŔZ�x���z�����E�w�̓���
�@�ɏW������B���̋��E�w�����f�������A�Z�x���z�����ł���Ƌߎ��������̂������ł���B
�Q�j �V���~�b�g��
����ƕ����ړ��̍��i��j��\�����ŁA���S�x�i�ˁ���/�ρj���g�U�W���c�Ŋ��������̂Ƃ��Ē�`�����B����́A����
�@���x�z���铮�S�x�ƕ����ړ����x�z����g�U�W���̂ǂ��炪���n�̒��ő傫�ȉe����^���Ă��邩��\�����̂ł���B
�R�j �t�B�b�N�̑��@��
�@�@����̓t�B�b�N�̑��@�����瓱�����A���ł���A���퍀���������̔Z�x�̎��Ԕ����ƈʒu�����Ƃ̊W�������B��
�@���Ō������퍀�Ƃ͕ω��ɂ���ď������鍀�ł���B�|�݂b/�݂����݂i/�݂��ɂi���|�c�݂b/�݂���������A
�@�@�@�@�@�@�@�@�@�@�@�@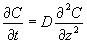
�@�ƂȂ�B
�@
��R �������ŁA���a����0.1mm�i���x�ρF2.7�~103kg���-3�j�̃K���X���������𗎉����Ă���B���ɒB�����Ƃ����I�����~���x�����߂�B�A���A���̖��x���v��1.0�~103kg���-3�A�S�x�ʂ�1.0�~10-3Pa����Ƃ���B
�q���g�F���q�����̂�����R�͂e�c�́A���C�W���b�c��p����
�e�c���b�c�(��2/�S)�(���v��2/�Q)
�����ŁA�b�c��24/�qe �i10-4���qe���Q�j
��10/�qe1/2 �i�Q���qe��500�j
��0.44 �i500���qe��105�j
�K���X���̎��ʂ��l�Ƃ���ƁA�l���ρ~�S��(���~10-3)3�^�R �i�A���A������/�Q�j�ł���A�K���X���������̂��鐅�̎��ʂ����Ƃ���ƁA�������v�~�S��(���~10-3)3�^�R�q���g����e�c�Ɖ����������̏d�́A���͂��ނ荇���Ă���̂ŁA�d�͉����x������9.8[��/��2]�Ƃ��A�����������𐳂Ƃ��āA�I�[���x����0�Ƃ���A
�O���l���|�e�c�|����
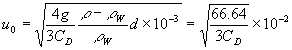 �@�@�c�c�c�i���j
�@�@�c�c�c�i���j
�����ŁA���C�m���Y����
�@�@�@�@�@�@�@�@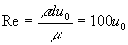
�ŗ^������̂ŁA�R�ɏꍇ��������B
�@�@�j�@10-4���qe���Q�@�܂�A10-6����0��0.02�@�̂Ƃ�
�@�@�b�c��24/�qe�Ȃ̂ŁA������i���j�ɑ������
�@�@�@�@�@�@�@�@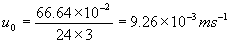
�@�@����͓��Ă͂܂�B
�@�A�j�@�Q���qe��500�@�܂�A0.02����0���T�@�̂Ƃ�
�@�@�b�c��10/�qe1/2�Ȃ̂ŁA������i���j�ɑ�����āA
�@�@�@�@�@�@�@�@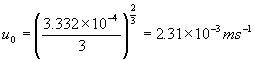
�@�@�ƂȂ�A����͕s�K
�@�B�j�@500���qe��105�@�܂�A�T����0��103�@�̂Ƃ�
�@�@�b�c��0.44�Ȃ̂ŁA������i���j�ɑ�����āA
�@�@�@�@�@�@�@�@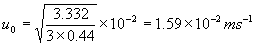
�@�@�ƂȂ�A������s�K
�@�ȏ���A��0��9.26�~10-3[��/��]�ƂȂ�B
�@
��S �������k�ŕ����\���傫�ȕ��������Q�q���u�ĂĂ�����Ă���B���̋�ԓ���S�x�ʂ̗��̂�����Ă���B����Ԃ����肵�āA�ȉ��̐ݖ�ɓ�����B
�@�@�@���j���̖��͉~�Ǔ��̑w���Ɠ����悤�Ɏ�舵���Ă��������B�ڍׂ͑��x�_��79�y�[�W
- ��Ԃ̒��S���炒�̈ʒu�Ɍ��������A�����k�̑w���l���āA���̑w�Ɋւ���^���ʂ̎��x���𗧂Ă�B�A���A�Ǔ�������яo���̈��͂����ꂼ��oin�A�oout�i���o���oin�|�oout�j�A�w��������ъO���̙��f���͂����ꂼ������A�����{�����Ƃ���B
�@���x���́i���̗����ɓ����O�́j���i���Ƃ��{�����̊Ԃ̙��f���́j�Ȃ̂ŁA���̕����v�Ƃ��āA
�@�@�@�@�@�@�����v(�oout�|�oin)���Q(�v�k�����|�v�k�����{����)
�@�@�@�@�@�@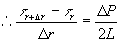
- �������O�Ƃ��āA�P�j�̎��x��������������ɕϊ�����B
�@�@�@�@�@�@�������O�Ƃ��āA�@�@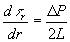
- ���f���̓т��ANewton�̖@����p���Ď������̑��x���̌��z�ŕ\���A�Q�j�̔������������������ɂ��A��ԓ��̑��x���z���B���E�������@�j��Ԃ̒��S�ł̙��f���̓т͂O�ł��邱�ƁA�A�j�Ǖǂł̗��������O�ł��邱�Ƃ̂Q�_�ł���B
�@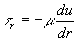 �@�ƕ\����A�Q�j�̔����������������ƁA�@
�@�ƕ\����A�Q�j�̔����������������ƁA�@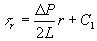 �@�Ȃ̂ŁA�����Newton�̖@�����������
�@�Ȃ̂ŁA�����Newton�̖@�����������
�@�@�@�@�@�@�@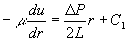 �@�@�@�́@�@�@
�@�@�@�́@�@�@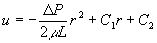 �@�@�@�@�i�b1�A�b2�͐ϕ��萔�j
�@�@�@�@�i�b1�A�b2�͐ϕ��萔�j
����ɋ��E�����������āA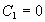 �A
�A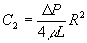 �@�Ȃ̂ŁA
�@�Ȃ̂ŁA
�@�@�@�@�@�@�@�@�@�@�@�@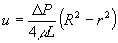
- �R�j�ŋ��߂���ԓ��̑��x���z��ϕ����鎖�ɂ��A���ϗ��������������߂�B
�@���͋ψ�Ȃ̂ŖʐςłȂ�������͈̔͂��l����B
�@�@����������Q�������^�Q�q����A

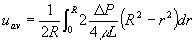
�@�@�@ �@�@�@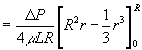
�@�@�@ �@�@�@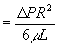
- ���ϗ����������ƍő嗬�����l�����Ƃ̊W�����߂�B
�@�@�@�@�@�@�@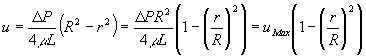
�@�ł���̂ŁA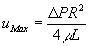 �@�ƂȂ�A
�@�ƂȂ�A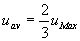
�@
��T�@���a����5.0cm�ŁA�����k��50���̉~�ǂ̓��ǂ�50���ɕۂ���Ă���B���̒��ω��x40���̐���2.0��/���ŗ���Ă���Ƃ��̉~�ǂ��琅�ւ̓`�M���x�i�P�ʎ��ԓ�����̑��`�M�ʁj�����߂�B�A���A���̖��x�ρ�1.0�~103kg���-3�A
�S�x�ʁ�1.0�~10-3Pa����A�M�`���x�i�M�`�����j�ȁ�0.63�i��-1��-1�j-1�A��M�b����4.2�~103�ikg-1�j-1�͉��x�Ɉ˂炸���ł���Ɖ��肷��B�Ȃ��A�w���̂Ƃ��@�mu��1.4[�qe�or{��/(�Q�k)}]1/3
�@�@�@�@�@�@�@�@�@�@�����̂Ƃ��@�mu��0.35�qe7/12[�or{��/(�Q�k)}]1/5
�@�@�@�@�@�@�@�@�@�@�A���A�@�mu������/��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�or���ʂb��/�ȁ@�@�@�@�Ƃ���B
�@���C�m���Y���́@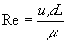 �@�ł���������̂ŁA������v�Z���Ăqe��1.0�~108��4000�ƂȂ�A�~�Ǔ��𗬂��̂͗����Ɣ��f�����B����ɂ��A�mu������/�ȂƂor���ʂb��/�Ȃ��mu��0.35�qe7/12 [�or{��/(�Q�k)}]1/5�ɑ������������܂�A
�@�ł���������̂ŁA������v�Z���Ăqe��1.0�~108��4000�ƂȂ�A�~�Ǔ��𗬂��̂͗����Ɣ��f�����B����ɂ��A�mu������/�ȂƂor���ʂb��/�Ȃ��mu��0.35�qe7/12 [�or{��/(�Q�k)}]1/5�ɑ������������܂�A
�@�@�@�@�@�@�@�@�@�@�@�@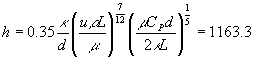 [�i��-2��-1�j-1]
[�i��-2��-1�j-1]
�ƂȂ�B���߂���̂͒P�ʎ��ԓ�����̑��`�M�ʂȂ̂ŁA�t���b�N�X�ɖʐς��|����悢�B���ǂ̕\�ʐς��r�Ƃ���A
�r�����k�ƂȂ�A�t���b�N�X�A�`�M���x�����ꂼ�ꂑ�A�p�Ƃ���A
�@�@�@�@�@�@�@�@�@�@�@�@���������s
�@�@�@�@�@�@�@�@�@�@�@�@�p�����~�r
�@�@�@�@�@�@�@�@�@�@�@�@�@�������s���k
�@�@�@�@�@�@�@�@�@�@�@�@�@��1163.3�~10�~3.14�~5.0�~10-2�~50
�@�@�@�@�@�@�@�@�@�@�@�@�@��9.13�~104�i��-1
�@
![]()
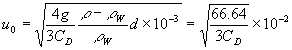 �@�@�c�c�c�i���j
�@�@�c�c�c�i���j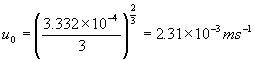
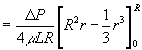
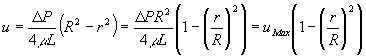
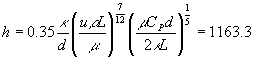 [�i��-2��-1�j-1]
[�i��-2��-1�j-1]